Профессор Шихаев К.Н., лауреат государственной премии СССР и премии Совета Министров СССР
- Уравнение Ферма
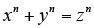, стоящее в тождествах фигурных прямоугольных чисел, «как фигурное прямоугольное число»:
(1), не может иметь целочисленных решений, поскольку фигурные числа не могут иметь нолей, а предположение о возможности целочисленного решения уравнения Ферма, даёт условие: Сравнение 
, чего не может быть.
- Аналогичные решения уравнения Ферма даёт его выражение в тождествах фигурных треугольных чисел, «как фигурное треугольное число»:
. (2)
- Решения уравнения Ферма (1) и (2) получены согласно моих формул:
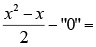фигурные треугольные числа 
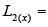1,3,6,10,15,21,28,… и так до бесконечности, что есть свойство фигурных чисел.
фигурные прямоугольные числа =1,4,10,20,35,56,84,120,… и так до бесконечности.
У нас есть и другие решения уравнения Ферма. Но главное: Получен учебный курс по уравнениям теории чисел, в том числе Ферма в фигурных числах, который не сложнее (но проще) чем обычные курсы по теории чисел. Ждём заказ.